Test

Documentation of the demonstration cases located in test.

Transfinite Mesh interTransMesh

Create a simple geometry by an intersection of two curves and mesh a four sided face with quadrangles.

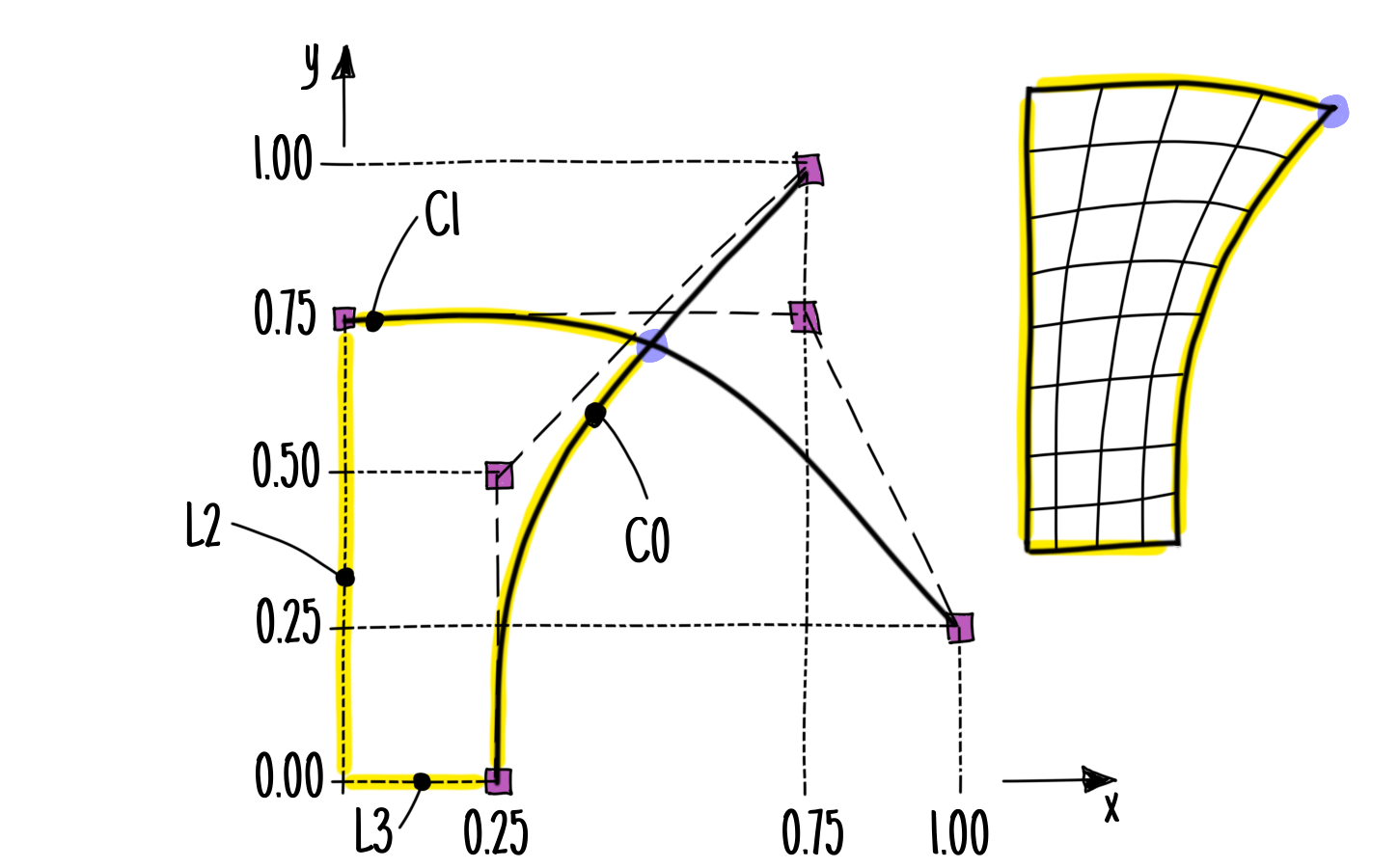
Fig. 9 Sketch of geometry and mesh including control points (magenta colored), B-Splines (black thick solid), intersection point (magenta colored), and mesh face’s boundaries (yellow colored); transfinite mesh shown on the right hand side

Import dtOO:

>>> import dtOOPythonSWIG as dtOO

Define dtOO’s options:

>>> dtOO.staticPropertiesHandler.getInstance().jInit(
...   dtOO.jsonPrimitive(
...     '{'
...       '"option" : ['
...         '{"name" : "reparamOnFace_precision", "value" : "1.e-05"},'
...         '{"name" : "reparamInVolume_precision","value" : "1.e-05"},'
...         '{"name" : "invY_precision", "value" : "1.e-04"},'
...         '{"name" : "xyz_resolution", "value" : "1.e-05"},'
...         '{"name" : "XYZ_resolution", "value" : "1.e-04"},'
...         '{"name" : "uvw_resolution", "value" : "1.e-04"},'
...         '{"name" : "point_render_diameter", "value" : "0.005"},'
...         '{"name" : "vector_render_size", "value" : "0.05"},'
...         '{"name" : "function_render_resolution_u", "value" : "21"},'
...         '{"name" : "function_render_resolution_v", "value" : "21"},'
...         '{"name" : "function_render_resolution_w", "value" : "21"},'
...         '{"name" : "geometry_render_resolution_u", "value" : "21"},'
...         '{"name" : "geometry_render_resolution_v", "value" : "21"},'
...         '{"name" : "geometry_render_resolution_w", "value" : "21"},'
...         '{"name" : "ompNumThreads", "value" : "2"},'
...         '{"name" : "map1dTo3d_deltaPer", "value" : "0.01"},'
...         '{"name" : "map2dTo3d_deltaPer", "value" : "0.01"},'
...         '{"name" : "map3dTo3d_deltaPer", "value" : "0.01"},'
...         '{"name" : "logLevel", "value" : "0"},'
...         '{"name" : "isEqualExtendCheck", "value" : "false"}'
...       ']'
...     '}'
...   )
... )

Create a log file:

>>> dtOO.logMe.initLog('interTransMesh.log')
'interTransMesh.log'

Create a dtBundle object; this is necessary for the definition of a labeledVectorHandlingConstValue object that is observed by a dtOO.lVHOstateHandler.clear:

>>> container = dtOO.dtBundle()
>>> cV = container.cptr_cV()
>>> dtOO.lVHOstateHandler.clear()
>>> dtOO.lVHOstateHandler( dtOO.jsonPrimitive(), cV).thisown = False

Create a B-Spline curve with three control points and of second order; the __lshift__- or <<-operator appends the points to the vectorDtPoint3 object:

>>> C0 = dtOO.bSplineCurve_pointConstructOCC(
...   dtOO.vectorDtPoint3()
...     << dtOO.dtPoint3(0.25,0.00,0.00)
...     << dtOO.dtPoint3(0.25,0.50,0.00)
...     << dtOO.dtPoint3(0.75,1.00,0.00),
...   2
... ).result()

Create a second B-Spline curve:

>>> C1 = dtOO.bSplineCurve_pointConstructOCC(
...   dtOO.vectorDtPoint3()
...     << dtOO.dtPoint3(0.00,0.75,0.00)
...     << dtOO.dtPoint3(0.75,0.75,0.00)
...     << dtOO.dtPoint3(1.00,0.25,0.00),
...   2
... ).result()

Create a minimization object to find the intersection point of two curves; the object is created with a subclass of floatAtt; different choices are implemented in attributionHeaven; the class curveCurveDist calculates the distance of two points that are on two different curves:

>>> gmf = dtOO.gslMinFloatAttr(
...   dtOO.curveCurveDist(C0,C1),
...   dtOO.vectorReal([0.5, 0.5,]),
...   dtOO.vectorReal([0.001, 0.001,]),
...   1.e-8,
...   100
... )

Perform the minimization; the result is stored in an internal vector that can be accessed via the result() function:

>>> gmf.perform()
True

Create the B-Spline surface; the builder bSplineSurface_bSplineCurveFillConstructOCC takes four curves as input and constructs a B-Spline surface; the boundary curves are constructed as straight line (L3 and L2 in Fig. 9) or trimmed curve (pieces of C0 and C1 in Fig. 9):

>>> S0 = dtOO.bSplineSurface_bSplineCurveFillConstructOCC(
...   dtOO.bSplineCurve_pointConstructOCC(
...     dtOO.dtPoint3(0,0,0), C0.pointPercent(0.0)
...   ).result(),
...   dtOO.trimmedCurve_uBounds(
...     C0, 0.0, C0.u_uPercent(gmf.result()[0])
...   ).result(),
...   dtOO.trimmedCurve_uBounds(
...     C1, 0.0, C1.u_uPercent(gmf.result()[1])
...   ).result(),
...   dtOO.bSplineCurve_pointConstructOCC(
...     dtOO.dtPoint3(0,0,0), C1.pointPercent(0.0)
...   ).result()
... ).result()

Create an analyticSurface:

>>> aS0 = dtOO.analyticSurface(S0)

Create a gmshBoundedVolume for meshing:

>>> gBV = dtOO.gmshBoundedVolume()

Initialize the boundedVolume:

>>> gBV.jInit(
...   dtOO.jsonPrimitive(
...   '{'
...     '"label" : "interTransMesh", '
...     '"option" : ['
...       '{"name":"[gmsh]General.Terminal", "value":"1."},'
...       '{"name":"[gmsh]General.Verbosity", "value":"0"},'
...       '{"name":"[gmsh]General.ExpertMode", "value":"1."},'
...       '{"name":"[gmsh]Mesh.LcIntegrationPrecision", "value":"1.0E-04"},'
...       '{"name":"[gmsh]Mesh.CharacteristicLengthMin", "value":"0.1"},'
...       '{"name":"[gmsh]Mesh.CharacteristicLengthMax", "value":"0.5"},'
...       '{"name":"[gmsh]Mesh.Algorithm", "value":"1"},'
...       '{"name":"[gmsh]Mesh.MeshSizeExtendFromBoundary", "value":"1"},'
...       '{"name":"[gmsh]Mesh.MeshSizeFromPoints", "value":"1"}'
...     '],'
...     '"analyticGeometry" : []'
...   '}'
...   ),
...   None, None, None, None, None
... )

Store the underlying gmsh model in gm:

>>> gm = gBV.getModel()

Add the analyticSurface and tag the face with a string:

>>> gm.tagPhysical(
...   gm.getDtGmshFaceByTag(gm.addIfFaceToGmshModel( aS0 )), "theFace"
... )

Define the B-Spline surface as transfinite face and recombine the triangles:

>>> gm.getDtGmshFaceByPhysical("theFace").meshTransfinite()
>>> gm.getDtGmshFaceByPhysical("theFace").meshRecombine()

Define all boundary curves of the face as transfinite faces and define an uniform point distribution:

>>> gm.getDtGmshEdgeByPhysical("theFace->0").meshTransfinite(1,1)
>>> gm.getDtGmshEdgeByPhysical("theFace->1").meshTransfinite(1,1)
>>> gm.getDtGmshEdgeByPhysical("theFace->2").meshTransfinite(1,1)
>>> gm.getDtGmshEdgeByPhysical("theFace->3").meshTransfinite(1,1)

Set the number of elements on the boundary edges:

>>> gm.getDtGmshEdgeByPhysical("theFace->0").setNElements(5)
>>> gm.getDtGmshEdgeByPhysical("theFace->1").setNElements(10)
>>> gm.getDtGmshEdgeByPhysical("theFace->2").setNElements(5)
>>> gm.getDtGmshEdgeByPhysical("theFace->3").setNElements(10)

Define and initialize a mesh rule with mesh operators:

>>> ob = dtOO.bVOMeshRule()
>>> ob.jInit(
...   dtOO.jsonPrimitive(
...     '{'
...       '"_rule1D" : ["dtMeshGEdge(theFace->*)"],'
...       '"_rule2D" : ["dtMeshGFace(theFace)"],'
...       '"_rule3D" : [],'
...       '"_only" : [],'
...       '"dtMeshOperator" : ['
...         '{"name" : "dtMeshGEdge","label" : "dtMeshGEdge"},'
...         '{"name" : "dtMeshGFace", "label" : "dtMeshGFace"}'
...       ']'
...     '}'
...   ),
...   None, None, None, None, None, gBV
... )

Attach the observer to the gmshBoundedVolume; set thisown flag to prevent segmentation fault:

>>> gBV.attachBVObserver(ob)
>>> ob.thisown = False

Create the mesh:

>>> gBV.makeGrid()

Create and initialize an observer to write the mesh to a msh file:

>>> ob = dtOO.bVOWriteMSH()
>>> ob.jInit(
...   dtOO.jsonPrimitive(
...     '{"_filename" : "interTransMesh.msh", "_saveAll" : true}'
...   ),
...   gBV
... )

Apply the observer to write the mesh:

>>> ob.postUpdate()

Minimization floatAtt

Import

>>> from dtOOPythonSWIG import *

Create staticPropertiesHandler and initialize:

>>> staticPropertiesHandler.getInstance().jInit(
...   jsonPrimitive(
...     '{'
...       '"option" : ['
...         '{"name" : "reparamOnFace_precision", "value" : "1.e-06"},'
...         '{"name" : "reparamInVolume_precision","value" : "1.e-06"},'
...         '{"name" : "invY_precision", "value" : "1.e-04"},'
...         '{"name" : "xyz_resolution", "value" : "1.e-08"},'
...         '{"name" : "XYZ_resolution", "value" : "1.e-07"},'
...         '{"name" : "uvw_resolution", "value" : "1.e-04"},'
...         '{"name" : "logLevel", "value" : "99"},'
...         '{"name" : "map2dTo3d_deltaPer", "value" : "1.e-8"}'
...       ']'
...     '}'
...   )
... )

Initialize a log file:

>>> logMe.initLog("floatAtt.log")
'floatAtt.log'

Create the function

\[ff: (u,v) \rightarrow (u,v,u^2+v^2)\]

as a vec3dMuParserTwoD-object:

>>> ff = vec3dMuParserTwoD("u,v,u*u+v*v","u","v")

Set the ranges for \(u\) and \(v\):

>>> for i in [0,1,]:
...   ff.setMin(i,-100.0)
...   ff.setMax(i,+100.0)

Create the infinite space \(im\) as parameter space for the function \(ff\):

>>> im = infinityMap3dTo3d()

Define an analyticGeometry as a composition of \(ff\) and \(im\):

>>> mm = vec3dTwoDInMap3dTo3d(ff,im)

Define the point \(p0\) that should be reparameterized:

>>> p0 = dtPoint3(0,0,0)

Define a pointGeometryDist object that provides the connection between the analyticGeometry \(mm\) and the point \(p0\); pointGeometryDist is a strategy for ``floatAtt`:

>>> att = pointGeometryDist(p0, mm)

Minimize the distance between geometry and point using a gradient-based minimization technique; the attributes of the minimizer are the strategy, the initial guess, the step size, the desired precision, and the maximum number of iterations:

>>> gradMin = gslGradMinFloatAttr(
...   att,
...   [0.01,.99],
...   [0.001,0.001],
...   1.e-8,
...   100
... )

Convergence check:

>>> gradMin.perform()
True

Minimize the distance using a gradient-free minimization technique:

>>> min = gslMinFloatAttr(
...   att,
...   [0.01,.99],
...   [0.001,0.001],
...   1.e-8,
...   100
... )

Convergence check:

>>> min.perform()
True

Simple Axial Runner simpleAxialRunner

Create a very simple machine that consists only of an axial runner. First an object is created by:

>>> machine = simpleAxialRunner()

The channel is created by two splines each containing two control points. Within the channel a mean plane is defined and a thickness distribution is added. The machine is created by:

>>> bundle = machine.create(alpha_2_1=40.0)

This results in a machine with an outlet angle at the shroud of 40 degree.

The OpenFOAMCase is created by:

>>> bundle.cptr_dC()["of"].runCurrentState()

The current case is then written to a directory:

>>> cDir = bundle.cptr_dC()["of"].getDirectory(
...   dtOO.lVHOstateHandler().commonState()
... )

The foamlib package is used to modify the dicts.

>>> import foamlib

Initialize foamlib object

>>> fc = foamlib.FoamCase( cDir )

Before running the simulation the writeInterval and endTime is adjusted by:

>>> fc.control_dict['writeInterval'] = 25
>>> fc.control_dict['endTime'] = 50

Additionally, the flow is treated as laminar:

>>> fc.turbulence_properties["RAS"]["turbulence"] = False

The foamlib package is used to start the simulation:

>>> fc.run()
(of_...

dtOO.test.simpleAxialRunner.simpleAxialRunner.CreateAndShow(*args, **kwargs)

Create and show machine.

Parameters:

None

Returns:

• List[ dtOO.dtBundle, dtOOInParaVIEW ] – List containing the dtBundle and the render object for ParaVIEW.

• See Also

• ———

• simpleAxialRunner.create (Create machine.)

class dtOO.test.simpleAxialRunner.simpleAxialRunner.simpleAxialRunner

Simple machine consisting of an axial runner only.

Parameters:

None

create(alpha_1_0: float = 90.0, alpha_1_1: float = 90.0, alpha_2_0: float = 80.0, alpha_2_1: float = 80.0) → dtOOPythonSWIG.dtBundle

Create machine.

The machine is created and dtOO’s logfile is created as build.log.

Parameters:

• alpha_1_0 (float, default = 90.0) – Inlet angle at hub.

• alpha_1_1 (float, default = 90.0) – Inlet angle at shroud.

• alpha_2_0 (float, default = 80.0) – Outlet angle at hub.

• alpha_2_1 (float, default = 80.0) – Outlet angle at shroud.

Returns:

Container that contains machine’s parts.

Return type:

dtContainer