Demonstration

Documentation of the demonstration cases located in demo.

Kinetic Turbine canada

The free-flow machine is shown in Fig. 1. The entire diffuser and the shrouding in the guide vane and runner area have a constant wall thickness. The guide vanes in the figure (top left) are arranged downwards and have a V-shape with an angle of 72°. The runner blades are positioned next to them in downstream direction. The diffuser has a constant maximum height. Therefore, the arrangement of the three-parted diffuser has no section projected to the flow direction in the upper and lower areas. The figure shows the vents oriented towards the axis of rotation in the upper area (top right) and the vents pointing away from the axis of rotation on the side (bottom left). The edges at the end of a corresponding diffuser section is straight. The hub is spherical in front of the guide vane inlet and conical at the diffuser inlet. For the design, only runner and diffuser are variable; the guide vane is fixed and does not direct the flow. As a result, the inflow to the runner is swirl-free.

Fig. 1 Three-dimensional representation of the kinetic turbine (top left) with two guide vanes arranged at the bottom and four rotor blades; diffuser is designed in three parts; machine’s side view without blades (top right); view from the front (bottom left); top view without blades (bottom right)

Fig. 2 shows a simulation result of an optimized machine. The streamlines are coloured with the velocity magnitude. Backflow regions are visulaized as magenta coloured iso volumes. According to figure Fig. 2, the flow enters the machine through the inlet section and, additionally, through the vents. Behind the hub only small vortices occur. The flow follows the opening of the diffuser. According to theoretical considerations, the optimized machine shows a flap at the end of the third diffuser section.

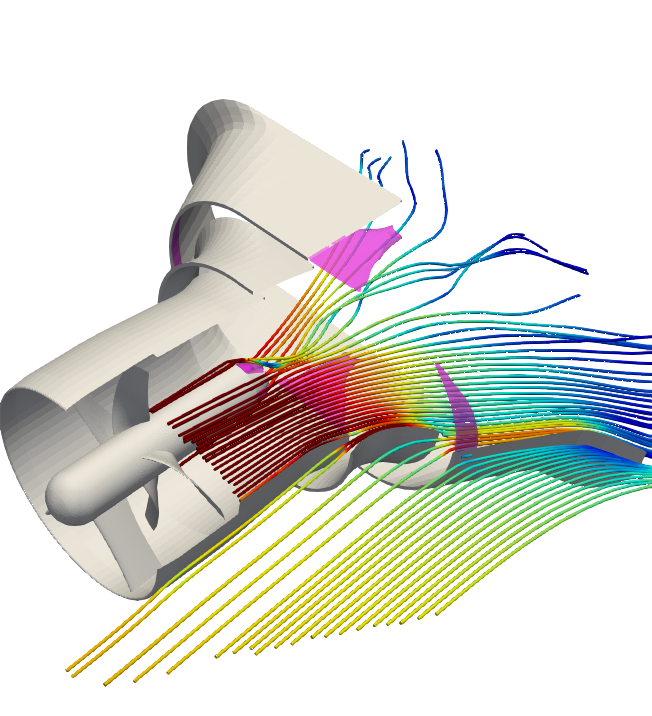
Fig. 2 Three-dimensional representation of the kinetic turbine including the simulated flow field; streamlines are coloured with the velocity magnitude from low (blue) to high (red); backflow volume shown as magenta coloured iso volume;

[Tismer_2020] contains a more detailed description including a documented optimization. [Mastaller_2023] gives additional theoretical background and unsteady simulation results of an optimized candidate.

Parameterization

Fig. 3 shows the parameterization of the diffuser geometry. The guide vane and runner area is marked by the rectangle drawn as a dash-dot line. For the design of the kinetic turbine, the control points shown are fixed (empty rectangles) or movable (filled rectangles). Each gray edge of the diffuser is defined by a B-spline of second order. The first and last spline each have three movable and one fixed control point. The former fulfills the constraint of a smooth transition from the guide vane and runner area to the diffuser shape, the latter limits the horizontal (\(x\)-direction) expansion of the diffuser. The transition from guide vane and runner area to the diffuser is made differentiable by fixing the second control point in the \(x\)-direction. All three control points in the second diffuser section can move. The first point at each of the first and third diffuser part can only be move in the \(x\)-direction. The overlap in \(z\)-direction of the parts is fixed. Overall, the diffuser is parameterized with \(15\) degrees of freedom (DOF). In the following, DOFs in the \(x\)-direction are denoted by \(E_{p,q}\) and in the \(z\)-direction by \(L_{p,q}\). With the index \(p\), the first, second and third diffuser section is characterized by the indices \(0\), \(1\) and \(2\), respectively. The second index \(q\) corresponds to the first to fourth and first to third control points per diffuser part by the indices \(0.0\), \(1.0\), \(1.5\) and \(2.0\) and \(0.0\), \(1.0\) and \(2.0\), respectively.

Fig. 3 also contains parts of the unstructured mesh blocks (black solid line). The remaining space within the investigated area (black dotted line) is meshed with a block structured grid. In this case, the hybrid mesh reduces the number of cells and the complexity of the block structure. An adequate number of elements is required upstream and downstream of the hub, which is, in case of a pure block structured approach, completely imprinted on the inflow section. Due to the small hub in relation to the diffuser, fewer elements are generally required near the hub than on the diffuser. The unstructured areas decouple the mesh. In addition, the geometric deformation of the diffuser mesh in the \(x\)-direction can be compensated by tightening the inner blocks. This results in more tetrahedral elements; at the same time, the hexahedrons remain more uniform in the structured areas.

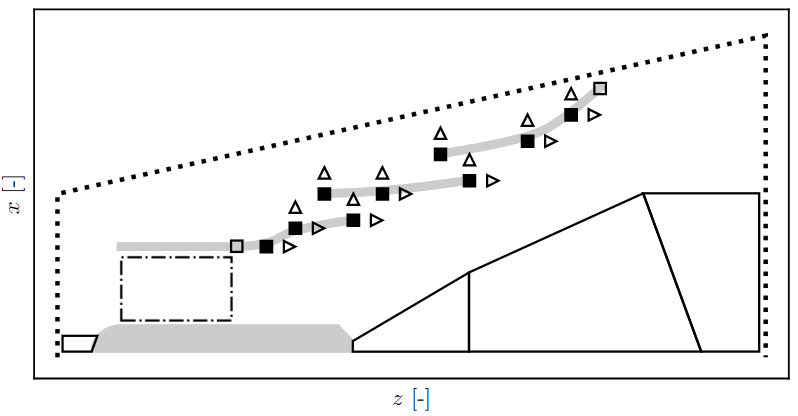
Fig. 3 Schematic representation of the kinetic turbine in half-sided view with boundaries (gray) and the bladed space (black dash-dotted line); control points (rectangles) are fixed (empty) or moveable (filled); unstructured grid blocks drawn as black solid line; coupling (black dotted line) to the coarsely meshed far-field via a general grid interface

Fig. 4 contains the parameterization of a mid-surface section for the runner. Each section is defined by four DOFs. The outlet angle \(\beta_o\) and the position (sickling) in the circumferential direction \(\phi r_o\) can be changed. The index \(o\) defines the position of the cut in the spanwise direction. The distribution of the thickness is

(1)\[y(t,T) = T \left( 0.2969 \sqrt{t} − 0.1260 t − 0.3516 t^2 + 0.2843 t^3 − 0.1015t^4 − 0.0021t^4 \right)\]

where \(t\) follows the parameter value of the meanline. Additionally, the parameter \(X\) (not shown in figure) shifts the maximum thickness \(T\) to the inlet or outlet. This means that only symmetrical thickenings can be generated.

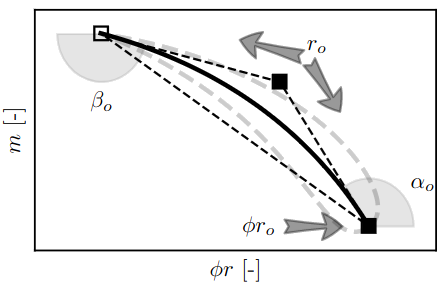
Fig. 4 Control polygon (black dashed) of the center line (black solid) with fixed (empty) and movable (filled) control points; entry and exit angles \(\alpha_o\) and \(\beta_o\) as well as deflection \(r_o\) can be changed; position of the cut in circumferential direction can be changed via DOF \(\phi r_o\)

The runner blade is generated from three sections parameterized according to Fig. 4. Fig. 5 shows a schematic sketch of the three-dimensional blade. Visible edges are shown as thick black lines, hidden edges as thin gray lines and mid-surface sections as dotted lines. The three directions \(\phi r\), \(m\) and \(r\) correspond to the arrows on the hub. The sections at the hub (\(s=0\)), center (\(s=0.5\)) and shroud (\(s=1\)) or index \(o=0\), \(o=1\) and \(o=2\) are connected by a B-Spline surface. According to Fig. 5, the span direction is not necessarily the radial direction.

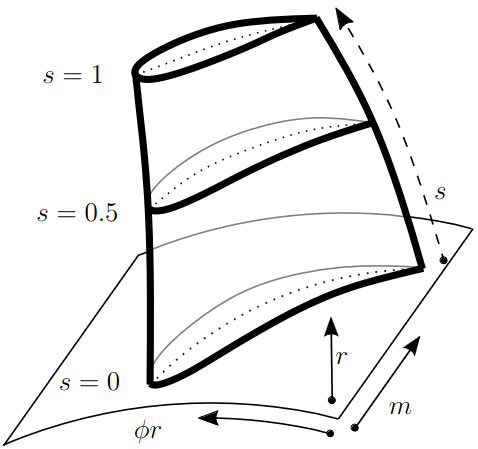
Fig. 5 Three-dimensional view of the impeller blade from three sections; hub section (thin black) with corresponding directional arrows; span direction of the blade (dashed directional arrow); visible (thick black) and hidden (thin gray) edges (solid); mean sections (dotted) shown for each section

The maximum thickening \(T\) of the mean line or mean surface from equation (1) is variable in spanwise direction. A blending

\[T(s) = T_0 + (T_1 - T_0) h(s)\]

with the blending function \(h(s)\) is defined by the fixed maximum thickenings \(T_0\) and \(T_1\) at the hub and shroud. Fig. 6 visualizes the function

\[h(s) = c_0 - c_1 \frac{ \mathrm{tanh} \left( G (sC - 1) \right) } { \mathrm{tanh}(G) }\]

with

\[c_0 = \frac{ \mathrm{tanh} G } { \mathrm{tanh} \left( G (C - 1) \right) + \mathrm{tanh} G }\]

and

\[c_1 = - \frac{\mathrm{tanh} G}{\mathrm{tanh} [G(C - 1)] + \mathrm{tanh} G}\]

for different parameter values of \(G\) and \(C\). For \(G = 0.01\) and \(C = 2\), the result is a linear blending that corresponds to the black dots. An increase in \(G\) bulges the blending symmetrically and makes it “s”-shaped according to the dashed lines from white to black. Changing \(C\) creates an asymmetrical blending in the direction of the hub or shroud (color gradient from dark to light). The steeper the gradient of \(h(s)\), the faster the change in thickening in the spanwise direction.

Fig. 6 Blending function of the thickness distribution; linear blending shown as black dots; variation of \(G\) and \(C\) shown by dashed lines and color gradient, respectively

Parameter symbols and labels

Table 1 gives the mapping between math symbols and constValue labels. Additionally, the min and max value for each DOF is shown. It is important to mention that all DOFs are scaled. Therefore, the values does not directly correspond to the dimension of an angle or a length.

Table 1 Mapping between math symbol and constValue label for DOFs including min and max values

Symbol	Label	Min	Max
\(r_0\)	cV_ru_ratio_0.0	0.05	0.8
\(r_1\)	cV_ru_ratio_0.5	0.2	0.9
\(r_2\)	cV_ru_ratio_1.0	0.2	0.8
\(\phi r_0\)	cV_ru_offsetPhiR_ex_0.0	-0.04	0.4
\(\phi r_1\)	cV_ru_offsetPhiR_ex_0.5	-0.04	0.4
\(\phi r_2\)	cV_ru_offsetPhiR_ex_1.0	-0.04	0.4
\(\alpha_1\)	cV_ru_alpha_1_ex_0.0	-0.2	0.3
\(\alpha_2\)	cV_ru_alpha_1_ex_0.5	-0.2	0.2
\(\alpha_3\)	cV_ru_alpha_1_ex_1.0	-0.2	0.2
\(\beta_1\)	cV_ru_alpha_2_ex_0.0	-0.2	0.3
\(\beta_2\)	cV_ru_alpha_2_ex_0.5	-0.2	0.3
\(\beta_3\)	cV_ru_alpha_2_ex_1.0	-0.2	0.2
\(\Delta L_{0,1}\)	cV_deltaL_dt_1	-0.10	0.6
\(\Delta L_{0,1.5}\)	cV_deltaL_dt_1.5	0.1	0.9
\(\Delta E_{0,1.5}\)	cV_deltaE_dt_1.5	0.05	0.7
\(\Delta E_{0,2}\)	cV_deltaE_dt_2	0.05	0.4
\(\Delta L_{1,0}\)	cV_deltaL_dt2_0	0.2	0.4
\(\Delta L_{1,1}\)	cV_deltaL_dt2_1	0.1	0.9
\(\Delta E_{1,0}\)	cV_deltaE_dt2_0	0.05	0.2
\(\Delta E_{1,1}\)	cV_deltaE_dt2_1	-0.10	0.9
\(\Delta E_{1,2}\)	cV_deltaE_dt2_2	0.1	0.9
\(\Delta L_{2,0}\)	cV_deltaL_dt3_0	0.3	0.72
\(\Delta L_{2,1}\)	cV_deltaL_dt3_1	0.1	0.9
\(\Delta E_{2,0}\)	cV_deltaE_dt3_0	0.05	0.1
\(\Delta E_{2,1}\)	cV_deltaE_dt3_1	-0.10	0.9
\(\Delta L_{2,1.5}\)	cV_deltaL_dt3_1.5	0.25	0.99
\(\Delta E_{2,1.5}\)	cV_deltaE_dt3_1.5	0.25	0.99
\(X\)	cV_thick_x	0.20	0.8
\(G\)	cV_thick_g	0.01	5.0
\(C\)	cV_thick_c_3	0.30	3.0

Simulation setup

The simulation area of the kinetic turbine consists of an area close to the turbine and a far-field. Fig. 7 shows the calculation area schematically. The far-field contains the dotted area near the turbine. A Dirichlet boundary condition for the velocity and a gradient boundary condition for the pressure are set at the inlet \((E)\); correspondingly, a gradient boundary condition and a Dirichlet boundary condition are specified at the outlet \((A)\). The connection of the near-field with the far-field is made via a generalized mesh interface at the coupling surfaces \((F_1, G_1)\), \((F_2, G_2)\) and \((F_3, G_3)\). By meshing the two areas separately, it is possible to mesh the far-field area more coarsely and, thus, save computation time. The two boundary surfaces at the top and bottom of the far-field (both summarized in \((N)\)) are defined as a frictionless wall. The detail at the bottom right of Fig. 7 shows the area close to the turbine with the guide vane and runner area as well as the subsequent diffuser. The guide vane, runner, hub and diffuser are only drawn in half section due to symmetry. All \((S)\) boundary surfaces are walls with a noslip condition. The part of the \((S)\) surface in the runner area (hub and blade) rotates according to the angular velocity. The coupling surface \((F_4, G_4)\) at the runner inlet is also a generalized mesh interface. There is a mixing plane interface between the guide vane and runner \((L_5, M_5)\) or runner and diffuser \((L_6, M_6)\).

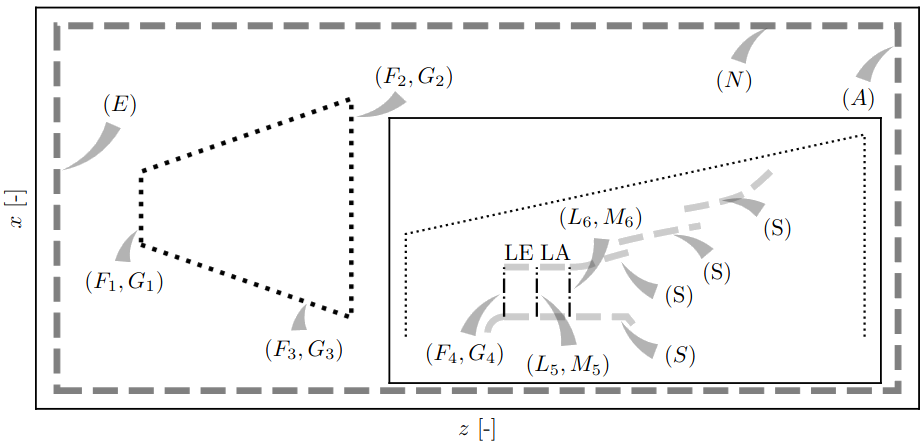
Fig. 7 Schematic representation of the simulation area consisting of near-field (dotted cone) and far-field (dashed rectangle); boundary conditions shown on boundary surfaces (letters without indices) and coupling surfaces (letters with indices); guide vane (LE) and runner (LA) area including diffuser and hub (both dashed gray) in detail

Running the case

Pull and run the latest stable container by:

docker pull atismer/dtoo:stable
docker run -it atismer/dtoo:stable

Change to the case directory by

cd /dtOO/demo/canada

and list the files in the directory by:

ls
E1_12685.xml  Mesh  build.py  geo  gmshMeshFile  init.xml  machine.xml  machineSave.xml  xml

The kinetic turbine is setup with the old XML (Extensible Markup Language) interface of the framework. Therefore, the main XML file machine.xml, the state files machineSave.xml and E1_12685.xml as well as the files located in directory xml are necessary to create the machine. The Mesh directory contains the fixed far-field mesh in CGNS format.

Using build.py

The Python script automatically creates the predefined state E1_12685 of the kinetic turbine. It is executed within the container by:

python3 build.py

Note

You have to set two MPI environment variables. This is necessary because within the container you are root. This has to be done before running any simulation by:

export OMPI_ALLOW_RUN_AS_ROOT=1
export OMPI_ALLOW_RUN_AS_ROOT_CONFIRM=1

Description of build.py

The first part of the script controls the framework. First the framework is imported with

from dtOOPythonSWIG import *

and the log file build.log is created with

logMe.initLog("build.log")

As previously mentioned, the kinetic turbine is created using the XML interface. The input and state XML file is loaded by the parser with

dtXmlParser.init("machine.xml", "E1_12685.xml")

and a reference to the parser is kept in the variable parser by

parser = dtXmlParser.reference()

Afterwards both XML files are parsed

parser.parse()

and the construction plan (XML files) of the machine is read. All objects are stored in STL (C++ Standard Template Library) like objects. And those objects have to be created for base ojects, DOFs, functions, geometries, mesh parts, simulation cases and plugins by, respectively,

bC = baseContainer()
cV = labeledVectorHandlingConstValue()
aF = labeledVectorHandlingAnalyticFunction()
aG = labeledVectorHandlingAnalyticGeometry()
bV = labeledVectorHandlingBoundedVolume()
dC = labeledVectorHandlingDtCase()
dP = labeledVectorHandlingDtPlugin()

before objects can be appended to the containers. All DOFs are created by the member function:

parser.createConstValue(cV)

The specific state (put simply: the values of the DOFs) is loaded to the DOFs by:

parser.loadStateToConst("E1_12685", cV)

All other objects are created by executing the command:

parser.destroyAndCreate(bC, cV, aF, aG, bV, dC, dP)

At this point, the complete machine is available within the containers. The last step is to create the meshes and setup the simulation case by:

dC.get("ingvrudtout_coupled_of").runCurrentState()

This step may take time, because the whole meshing procedure is performed.

The second part is the simulation of the flow field using OpenFOAM. In order to also handle this in Python, the PyFoam library is used. The import of the packages

from PyFoam.Applications.Decomposer import Decomposer
from PyFoam.Applications.WriteDictionary import WriteDictionary
from PyFoam.Applications.Runner import Runner
from PyFoam.Applications.ClearCase import ClearCase
from PyFoam.Applications.PackCase import PackCase

and definition of the case and state name

caseName = "ingvrudtout_coupled_of"
stateName = "E1_12685"

provides the necessary functions and attributes to correctly call PyFoam. For the kinetic turbine the simulation cases are created as folders according to the pattern:

ingvrudtout_coupled_of_<stateLabel>

<stateLabel> represents the name of the currently loaded state. At first, the case is decomposed by

Decomposer(
  args=[
    caseName+"_"+stateName,"4","--method=scotch","--clear","--silent"
  ]
)

and then ready to simulate the first 100 iterations as a laminar problem by:

WriteDictionary(
   args=[caseName+"_"+stateName+"/system/controlDict", "endTime", "100"]
 )
 WriteDictionary(
   args=[caseName+"_"+stateName+"/system/controlDict", "writeInterval", "100"]
 )
 WriteDictionary(
   args=[
     caseName+"_"+stateName+"/constant/turbulenceProperties",
     "RAS['turbulence']",
     "off"
   ]
 )
 Runner(
   args=[
     "--silent",
     "--autosense-parallel",
     "simpleFoam", "-case", caseName+"_"+stateName
   ]
 )

The second step is the simulation of the following 900 iterations as a turbulent problem by executing

WriteDictionary(
  args=[caseName+"_"+stateName+"/system/controlDict",
    "endTime", "1000"
  ]
)
WriteDictionary(
  args=[
    caseName+"_"+stateName+"/system/controlDict",
    "writeInterval", "1000"
  ]
)
WriteDictionary(
  args=[
    caseName+"_"+stateName+"/constant/turbulenceProperties",
    "RAS['turbulence']", "on"
  ]
)
Runner(
  args=[
    "--silent",
    "--autosense-parallel",
    "simpleFoam", "-case", caseName+"_"+stateName
  ]
)

and

Runner(
  args=[
    '--silent',
    'reconstructPar', '-latestTime', "-case", caseName+"_"+stateName
  ]
)

to reconstruct the parallel simulation case. The two commands

ClearCase(
  [
    '--keep-postprocessing',
    '--processors-remove',
    '--remove-analyzed',
    '--keep-postprocessing',
    '--clear-history',
    '--keep-last',
    caseName+"_"+stateName
  ])

and

PackCase([caseName+"_"+stateName, '--last'])

are optional. They clear and pack the simulation case. This is useful when performing an optimization to save disk space.

Creating an own state

The creation of a new state of the kinetic turbine starts with some already described functions of build.py. At first, the framework, the parser and the containers have to be defined by:

from dtOOPythonSWIG import *
logMe.initLog("build.log")
dtXmlParser.init("machine.xml", "E1_12685.xml")
parser = dtXmlParser.reference()
parser.parse()
bC = baseContainer()
cV = labeledVectorHandlingConstValue()
aF = labeledVectorHandlingAnalyticFunction()
aG = labeledVectorHandlingAnalyticGeometry()
bV = labeledVectorHandlingBoundedVolume()
dC = labeledVectorHandlingDtCase()
dP = labeledVectorHandlingDtPlugin()
parser.createConstValue(cV)

It is good practice to start from an existing state. Therefore, we use the E1_12685 state as initialization for all DOFs:

parser.loadStateToConst("E1_12685", cV)

At this point the DOFs are created and initialized. It can also be validated by:

parser.currentState()
>>> 'E1_12685'

The output is exactly the loaded state. We can start to modify any constValue listed in Table 1. One can easily iterate over all defined DOFs within a simple for-loop:

for i in cV:
  print(i.getLabel())
>>> cV_n
[...]
>>> cV_ru_alpha_1_ex_0.0
[...]
>>> cV_ru_stepNResplinePoints

Somewhere in the long list we found the inlet angle at the hub that is labelled as cV_ru_alpha_1_ex_0.0 according to Table 1. A call of the ()-operator

cV["cV_ru_alpha_1_ex_0.0"]()
>>> 0.04964900016784668

gives the current value of the DOF. We can change the angle by:

cV["cV_ru_alpha_1_ex_0.0"].setValue(0.05)

It is important to update the geometry of the runner mesh channel when the blade geometry is changed. Otherwise the mesh might not be correctly generated. The update is performed by:

dP.get("ru_adjustDomain").apply()

Put simply, the command adjusts other dependent DOFs to generate a valid mesh. Checking again the state by

parser.currentState()
>>> ''

shows that the current state is empty. We create a new state and validate that everything works correctly by:

parser.setState("iahr2024_state")
parser.currentState()
>>> 'iahr2024_state'

Optionally, we can extract the state and create a new state file by:

parser.extract("iahr2024_state", cV, "iahr2024_state.xml")

This creates the XML file iahr2024_state.xml within the directory. If no new file is desired, a call to

parser.write(cV)

inserts the new state in the currently loaded state file (E1_12685.xml). From this point, we can generate the whole machine by

parser.destroyAndCreate(bC, cV, aF, aG, bV, dC, dP)

and create the case directory by

dC.get("ingvrudtout_coupled_of").runCurrentState()

Of course, we also have to adjust the variable names, if we still use the above explained commands:

caseName = "ingvrudtout_coupled_of"
stateName = "iahr2024_state"

Additionally, we have to simulate the new case written in the directory ingvrudtout_coupled_of_iahr2024_state. This can be done with the above described commands of PyFoam.

Optimization of a Hydrofoil

This example optimizes a hydrofoil that is defined with 3 Degrees Of Freedom (DOFs). The optimization is performed with the differential evolution algorithm of scipy.

The fastest way to run the optimization of the hydrofoil is to execute:

pip install foamlib     && export OSLO_LOCK_PATH=/tmp     && export FOAM_SIGFPE=0     && python3.12 -m doctest build.py

Within the command foamlib is installed that is necessary to control OpenFoam in Python. The variable OSLO_LOCK_PATH defines the lock directory for oslo.concurrency. This should be a directory with fast I/O access. The second variable FOAM_SIGFPE is optional, but might be useful for preventing OpenFoam to fail with a floating point exception. Finally, this script is executed using the doctest module of Python.

The optimizer is imported from scipy and the interested reader is referred to [SciPy_2025]

>>> from scipy.optimize import differential_evolution

The callback function optimizeHydFoil of the optimizer executes all steps of the hydrofoil case. In the end, the fitness value of the hydrofoil is set as return value of the callback. Additionally, an exception handling catches all exceptions and returns a defined fitness value in case of an error.

>>> def optimizeHydFoil(x):
...   try:
...     hf = hydFoil( alpha_1=x[0], alpha_2=x[1], t_mid=x[2] )
...     hf.Geometry()
...     hf.GeometryMesh()
...     hf.Mesh()
...     hf.Simulate()
...     fit = hf.Evaluate()
...   except:
...     logging.warning("Catch Exception")
...     fit = hydFoil.FailedFitness()
...   return fit

Define the bounds of the DOFs for the optimization.

>>> bounds = [(150.0, 170.0), (155.0, 175.0), (0.01, 0.10),]

Call the optimizer with the callback function. The number of candidates is low to have a fast code example.

>>> result = differential_evolution(
...   optimizeHydFoil,
...   bounds,
...   popsize=3,
...   maxiter=2,
...   polish=False
... )

Output the final result of the optimization.

>>> logging.info(
...   "Optimum found at (alpha_1, alpha_2, t_mid) = (%f, %f, %f) with %f"
...   %
...   ( result.x[0], result.x[1], result.x[2], result.fun )
... )

class dtOO.demo.hydFoilOpt.build.hydFoil(alpha_1=100.0, alpha_2=130, t_mid=0.1)

Create, mesh, simulate and evaluate a hydrofoil.

This class holds all functions to create a hydrofoil with an inlet angle, outlet angle and a blade thickness. Fig. 8 shows a sketch of the hydrofoil.

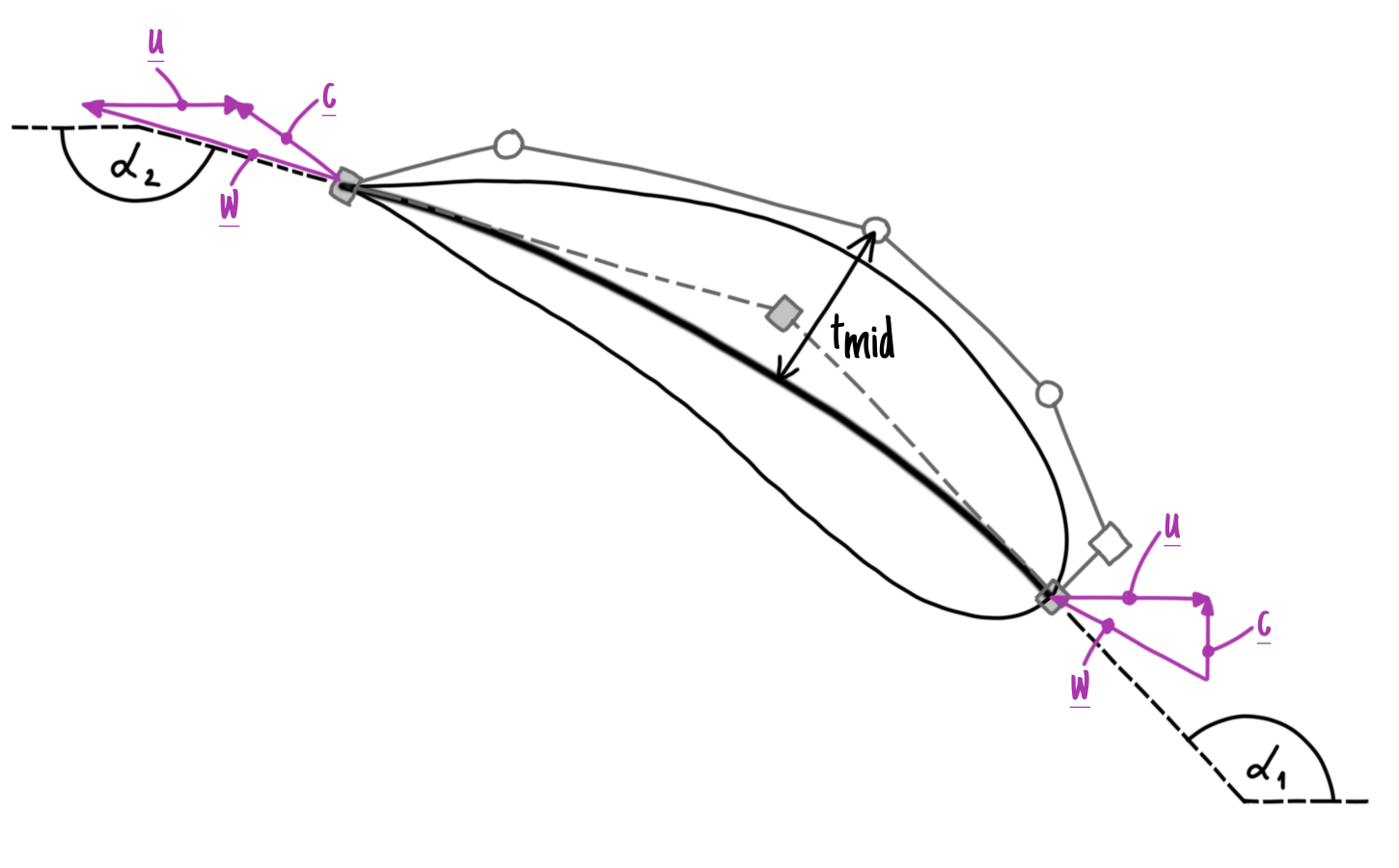
Fig. 8 Hydrofoil’s sketch including mean line (solid thick black line) and final shape (solid thin black line); B-Splines, that are used for constructing the meanline and final shape, are shown as solid and dashed gray thin lines; velocity triangles at inlet and outlet of the hydrofoil are colored in magenta; the DOFs, namely \(\alpha_1\), \(\alpha_2\), and \(t_{mid}\), are shown and labeled in black

The simulation of the hydrofoil is performed in the relational frame of reference. It means that all velocities in the CFD simulation correspond to \(w\). Therefore, when evaluating hydrofoil’s efficiency and head, the transformation

\[c = w + u = w + 2 \pi n R \approx w + 18.84 \frac{m}{s}\]

is necessary to get the absolute velocity \(c\). The hydrofoil is designed for a design head of \(0.8 m\). The fitness function is calculated based on head deviation and efficiency.

Parameters:

• alpha_1 (float) – Inlet angle.

• alpha_2 (float) – Outlet angle.

• t_mid (float) – Blade’s thickness.

Evaluate()

Evaluate the simulation.

The simulation is evaluated using the pyDtOO library. Additionally, the “patchToCsv” application is used to create csv files of the boundaries.

The fitness function is calculated based on head deviation and efficiency. Efficiency is given by the equation

\[\Delta \eta = 1 - \frac{F_y u}{\rho g H Q}\]

with \(F_y\), \(u\), \(\rho\), \(g\), \(H\), and \(Q\) that corresponds to force in \(y\)-direction, rotational speed, density, gravitational constant, simulated head, and discharge. The deviation in head is calculated by

\[\Delta H = \frac{|H-H_d|}{H_d}\]

with \(H_d\) that corresponds to design head. Then, the fitness value \(f\) is defined as:

\[f = \Delta H + \Delta \eta \mathrm{.}\]

It is clear: the lower the fitness function \(f\), the better the candidate.

Returns:

Fitness value of this candidate.

Return type:

float

static FailedFitness()

Failed fitness.

Returns the value that represents a failed design.

Returns:

Fitness for a failed design.

Return type:

float

Geometry()

Create hydrofoil’s geometry.

The main objects of baseContainer, analyticFunction, and analyticGeometry are created. Objects that are necessary or interesting are appended to the hydFoilOpt.build.hydFoil.bV, hydFoilOpt.build.hydFoil.aF, and hydFoilOpt.build.hydFoil.aG.

GeometryMesh()

Create additional hydrofoil’s geometry for meshing.

Create additional objects that are necessary for creating the mesh. These are mainly object’s of the mesh block that is created around the blade. This block is meshed as a structured block.

H_ = 0.2

Height of the mesh in \(m\).

Type:

float

L_ = 4.0

Length of the mesh in \(m\).

Type:

float

Mesh()

Create hydrofoil’s mesh.

Create the topology for the hydrofoil’s mesh. Additionally, define number of elements for edges and surfaces, define minimum and maximum element lengths for unstructured meshing algorithms, and label mesh parts.

R_ = 2.0

Radius of the blade cut in \(m\) where this hydrofoil is located.

Type:

float

Simulate()

Perform the simulation.

Perform the simulation using foamlib. The simulation runs for 500 iterations as a laminar simulation. Afterwards, it is switched to turbulent mode.

aF

Container object of dtOOPythonSWIG.analyticFunction.

Type:

dtOOPythonSWIG.labeledVectorHandlingAnalyticFunction

aG

Container object of dtOOPythonSWIG.analyticGeometry.

Type:

dtOOPythonSWIG.labeledVectorHandlingAnalyticGeometry

bC

base container.

Type:

dtOOPythonSWIG.baseContainer

bV

Container object of dtOOPythonSWIG.boundedVolume.

Type:

dtOOPythonSWIG.labeledVectorHandlingBoundedVolume

cV

Container object of dtOOPythonSWIG.constValue.

Type:

dtOOPythonSWIG.labeledVectorHandlingConstValue

c_mi_ = 5.77

Absolute velocity at inlet in \(\frac{m}{s}\)

Type:

float

container

Bundle object.

Type:

dtOOPythonSWIG.dtBundle

dC

Container object of dtOOPythonSWIG.dtCase.

Type:

dtOOPythonSWIG.labeledVectorHandlingDtCase

dP

Container object of dtOOPythonSWIG.dtPlugin.

Type:

dtOOPythonSWIG.labeledVectorHandlingDtPlugin

nB_ = 4

Number of blades in which this hydrofoil is located.

Type:

float

n_ = 90.0

Rotational speed in \(min^{-1}\).

Type:

float

state_

State label.

Type:

str

sys = <module 'sys' (built-in)>

Axial Runner tistos

Create, simulate, and evaluate an axial runner. This machine is the test case of [Eyselein_2025], [Rentschler_2024], [Raj_2024], and [Ebel_2024]. For the publication [Ebel_2024], the data set is provided in [axial_turbine_database]. This GitHub repository serves as the database for this demonstration case.

Run this tutorial by executing:

export OSLO_LOCK_PATH=/tmp && export FOAM_SIGFPE=0 \
  && python3.12 -m doctest build.py

Import logging package and create a configuration:

>>> import logging
>>> logging.basicConfig(
...     format='%(asctime)s %(levelname)s : %(message)s',
...     datefmt='%Y-%m-%d %H:%M:%S',
...     level=logging.INFO
... )

Import necessary classes from dtOO:

>>> from dtOOPythonSWIG import (
...   logMe,
...   dtXmlParser,
...   baseContainer,
...   labeledVectorHandlingConstValue,
...   labeledVectorHandlingAnalyticFunction,
...   labeledVectorHandlingAnalyticGeometry,
...   labeledVectorHandlingBoundedVolume,
...   labeledVectorHandlingDtCase,
...   labeledVectorHandlingDtPlugin,
...   lVHOstateHandler,
... )

Import packages from pyDtOO:

>>> from pyDtOO import (
...   dtScalarDeveloping,
...   dtForceDeveloping,
...   dtDeveloping
... )
>>> from pyDtOO import dtClusteredSingletonState as stateCounter

Import foamlib to control OpenFoam within Python:

>>> import foamlib

Import other default packages, necessary for evaluation and system calls:

>>> import numpy as np
>>> import sys
>>> import os

Clone repository [axial_turbine_database], if necessary:

>>> clone = "git clone https://github.com/ihs-ustutt/axial_turbine_database.git"
>>> if not os.path.isdir("./axial_turbine_database"):
...   logging.info("Clone repository.")
...   ret = os.system(clone)

Set up dtClusteredSingletonState configuration:

>>> stateCounter.PREFIX = 'T1'
>>> stateCounter.CASE = 'tistos_ru_of'
>>> stateCounter.DATADIR = './axial_turbine_database/runData'

Define the variables stored in the database:

>>> stateCounter.ADDDATA = [
...   'P',
...   'dH',
...   'eta',
...   'VCav',
...   'history',
...   'islandID',
... ]

Define default constructors for variables:

>>> stateCounter.ADDDATADEF = [
...   {"tl": 0, "n": 0, "vl": 0}, # P
...   {"tl": 0, "n": 0, "vl": 0}, # dH
...   {"tl": 0, "n": 0, "vl": 0}, # eta
...   {"tl": 0, "n": 0, "vl": 0}, # VCav
...   {}, # history
...   -1, # islandID
... ]

Define mapping between database’s parameters and constValue label. The parameters in runData are in the same sequence as the mapping:

>>> cVArr = [
...   {'label': 'cV_ru_alpha_1_ex_0.0', 'min': -0.155, 'max': 0.025},
...   {'label': 'cV_ru_alpha_1_ex_0.5', 'min': -0.19, 'max': -0.01},
...   {'label': 'cV_ru_alpha_1_ex_1.0', 'min': -0.19, 'max': -0.01},
...   {'label': 'cV_ru_alpha_2_ex_0.0', 'min': -0.08, 'max': 0.1},
...   {'label': 'cV_ru_alpha_2_ex_0.5', 'min': -0.08, 'max': 0.1},
...   {'label': 'cV_ru_alpha_2_ex_1.0', 'min': -0.08, 'max': 0.07},
...   {'label': 'cV_ru_offsetM_ex_0.0', 'min': 1.0, 'max': 1.5},
...   {'label': 'cV_ru_offsetM_ex_0.5', 'min': 1.0, 'max': 1.5},
...   {'label': 'cV_ru_offsetM_ex_1.0', 'min': 1.0, 'max': 1.5},
...   {'label': 'cV_ru_ratio_0.0', 'min': 0.4, 'max': 0.6},
...   {'label': 'cV_ru_ratio_0.5', 'min': 0.4, 'max': 0.6},
...   {'label': 'cV_ru_ratio_1.0', 'min': 0.4, 'max': 0.6},
...   {'label': 'cV_ru_offsetPhiR_ex_0.0', 'min': -0.15, 'max': 0.15},
...   {'label': 'cV_ru_offsetPhiR_ex_0.5', 'min': -0.15, 'max': 0.15},
...   {'label': 'cV_ru_offsetPhiR_ex_1.0', 'min': -0.15, 'max': 0.15},
...   {'label': 'cV_ru_bladeLength_0.0', 'min': 0.4, 'max': 0.8},
...   {'label': 'cV_ru_bladeLength_0.5', 'min': 0.6, 'max': 1.0},
...   {'label': 'cV_ru_bladeLength_1.0', 'min': 0.8, 'max': 1.3},
...   {'label': 'cV_ru_t_le_a_0', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_le_a_0.5', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_le_a_1', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_mid_a_0', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_mid_a_0.5', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_mid_a_1', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_te_a_0', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_te_a_0.5', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_t_te_a_1', 'min': 0.005, 'max': 0.06},
...   {'label': 'cV_ru_u_mid_a_0', 'min': 0.4, 'max': 0.6},
...   {'label': 'cV_ru_u_mid_a_0.5', 'min': 0.4, 'max': 0.6},
...   {'label': 'cV_ru_u_mid_a_1', 'min': 0.4, 'max': 0.6},
... ]

Initialize a dtClusteredSingletonState object for state 21260:

>>> sc = stateCounter(21260)

Create log file:

>>> logMe.initLog('build-'+sc.state()+'.log')
'build-T1_21260.log'

Initialize XML parser with construction and save file:

>>> parser = dtXmlParser.init("machine.xml", "machineSave.xml").reference()

Parse XML files:

>>> parser.parse()

Create basic container:

>>> bC = baseContainer()
>>> cV = labeledVectorHandlingConstValue()
>>> aF = labeledVectorHandlingAnalyticFunction()
>>> aG = labeledVectorHandlingAnalyticGeometry()
>>> bV = labeledVectorHandlingBoundedVolume()
>>> dC = labeledVectorHandlingDtCase()
>>> dP = labeledVectorHandlingDtPlugin()

Create constValue instances and load the templateState:

>>> parser.createConstValue(cV)
>>> parser.loadStateToConst("templateState", cV)

Iterate over all parameters from database and set the value in the correspoding constValue object. The array cVArr reuturns the correct label:

>>> cc = 0
>>> for anObj in sc.objective():
...   cV[ cVArr[cc]['label'] ].setValue( anObj )
...   cc = cc + 1

Create geometry, apply the ru_adjustDomain plugin, and create geometry again. The plugin adjusts the runner domain by changing the DOFs; therefore, it necessary to create the geometry twice:

>>> parser.destroyAndCreate(bC, cV, aF, aG, bV, dC, dP)
>>> dP.get('ru_adjustDomain').apply()
>>> parser.destroyAndCreate(bC, cV, aF, aG, bV, dC, dP)

Make a state in the container of constValue:

>>> lVHOstateHandler().makeState(sc.state())

Define empty dicts for power, head, efficiency, and cavitation volume:

>>> P = {}
>>> dH = {}
>>> eta = {}
>>> Vcav = {}

Create geometry, perform simulation, and perform evaluation for each operating point:

Note

Depending on the OpenFoam installation, it might be necessary to adjust the decomposition method, e.g. to

fc.decompose_par_dict['method'] = 'metis'

or any other method. As already mentioned, it depends on the current installation.

>>> for i in ["tl" , "n", "vl"]:
...   #
...   # Create OpenFoam case
...   #
...   dC.get('tistos_ru_of_'+i).runCurrentState()
...   #
...   # Initialize ``foamlib`` object; define parallel solution on 4
...   # processors; simulate 100 iterations laminar with a ``faceLimited``
...   # scheme
...   #
...   fc = foamlib.FoamCase( 'tistos_ru_of_'+i+'_'+sc.state() )
...   fc.decompose_par_dict['method'] = 'scotch'
...   fc.decompose_par_dict['numberOfSubdomains'] = 4
...   fc.control_dict['writeInterval'] = 100
...   fc.control_dict['endTime'] = 100
...   fc.turbulence_properties["RAS"]["turbulence"] = False
...   fc.fv_schemes['gradSchemes']['none'] = 'faceLimited Gauss linear 0.33'
...   fc.fv_schemes['gradSchemes']['grad(p)'] = 'faceLimited Gauss linear 0.33'
...   fc.fv_schemes['gradSchemes']['grad(U)'] = 'faceLimited Gauss linear 0.33'
...   fc.fv_schemes['divSchemes']['div(phi,U)'] = \
...     'Gauss linearUpwindV faceLimited Gauss linear 0.33'
...   fc.run()
...   #
...   # Simulate until 1000 iterations reached as a turbulent simulation with
...   # a ``cellLimited`` scheme
...   #
...   fc.control_dict['writeInterval'] = 1000
...   fc.control_dict['endTime'] = 1000
...   fc.turbulence_properties["RAS"]["turbulence"] = True
...   fc.fv_schemes['gradSchemes']['none'] = 'cellLimited Gauss linear 0.33'
...   fc.fv_schemes['gradSchemes']['grad(p)'] = 'cellLimited Gauss linear 0.33'
...   fc.fv_schemes['gradSchemes']['grad(U)'] = 'cellLimited Gauss linear 0.33'
...   fc.fv_schemes['divSchemes']['div(phi,U)'] = \
...     'Gauss linearUpwindV cellLimited Gauss linear 0.33'
...   fc.run()
...   #
...   # Reconstruct the case
...   #
...   fc.reconstruct_par()
...   #
...   # Extract the rotation speed from the case
...   #
...   omega = np.abs(
...     foamlib.FoamFile(fc.path/'constant/MRFProperties')['MRF_RU']['omega']
...   )
...   try:
...     #
...     # Read data from ``postProcessing`` folder
...     #
...     Q_ru_dev = dtScalarDeveloping(
...       dtDeveloping(str(fc.path/'postProcessing/Q_ru_in/100')).Read()
...     )
...     pIn_ru_dev = dtScalarDeveloping(
...       dtDeveloping(str(fc.path/'postProcessing/ptot_ru_in/100')).Read()
...     )
...     pOut_ru_dev = dtScalarDeveloping(
...       dtDeveloping(str(fc.path/'postProcessing/ptot_ru_out/100')).Read()
...     )
...     Vcav_dev = dtScalarDeveloping(
...       dtDeveloping(str(fc.path/'postProcessing/V_CAV/100')).Read()
...     )
...     F_dev = dtForceDeveloping(
...       dtDeveloping(str(fc.path/'postProcessing/forces')).Read(
...         {'force.dat' : ':,4:10', 'moment.dat' : ':,4:10', '*.*' : ''}
...       )
...     )
...     #
...     # Calculate power, head, efficiency, and cavitation volume; average
...     # simulation results over 100 iterations
...     #
...     P[i] = F_dev.MomentMeanLast(100)[2] * omega
...     dH[i] = (pOut_ru_dev.MeanLast(100) - pIn_ru_dev.MeanLast(100)) / 9.81
...     eta[i] = P[i] / (1000. * 9.81 * dH[i] * Q_ru_dev.MeanLast(100) )
...     Vcav[i] = Vcav_dev.MeanLast(100)
...     #
...     # Check if number of iterations reached and if it is a turbine not a
...     # pump
...     #
...     if fc[-1].name != '1000':
...       raise ValueError('Max number of iterations not reached.')
...     if np.abs(eta[i]) > 1:
...       raise ValueError('Pump detected.')
...   #
...   # Handle exceptions
...   #
...   except Exception as e:
...     logging.error('Catch exception : %s', e)

Compare simulation results with the results in the database. Accept an error of 1 %, otherwise report error:

>>> for valLab, valVar in zip(['P', 'dH', 'eta',],[P, dH, eta,]):
...   ref = sc.readDict(valLab)
...   for i in ['n', 'vl', 'tl',]:
...     diff = np.abs( (ref[i] - valVar[i]) / ref[i] )
...     logging.info("Difference for %s[%s] : %f %%" % (valLab, i, 100.*diff))
...     if diff > 0.01:
...       print("Difference for %s[%s] : %f %% > 1%%!" % (valLab, i, 100.*diff))